About Laplacian Mesh Optimization
Today I’ve read the paper “Laplacian Mesh Optimization” by Andrew Nealen, Takeo Igarashi, Olga Sorkine, Marc Alexa.
Mesh optimization and Smoothing
Mesh optimization is the reduction of the number of vertices in an initial mesh of triangles without change in the shape. And smoothing is to smooth surface by averaging or removing vertices that is significantly different from other vertices in mesh. Smoothing is performed by subdivision, but the number of vertices is kept in this study.
Novelty of the study
This study introduce a framework for triangle shape optimization and feature preserving smoothing of triangular meshes that is guided by the vertex Laplacians.
Method
Laplacian matrix and Laplacian of vertex
Mesh Graph(V is vertices, E is edges): $$G =\{V, E\}$$
vertices: $$V =[v_1^T, v_2^T,…, v_n^T]^T$$ $$v_i =[v_{ix}, v_{iy},v_{iz}]$$
x, y, z element of vertices: $$V_d =[v_{1d}, v_{2d},…, v_{nd}]^T$$ $$d \in \{x, y, z\}$$
Laplacian of vertex: $$\delta_i =\sum_{\{i,j\} \in E}w_{ij}(v_i, v_j)$$
Weight w is defined below: $$\sum_{\{i,j\} \in E}w_{ij} = 1$$ $$w_{ij} =\frac{\omega_{ij}}{\sum_{\{i,j\} \in E}\omega_{ij}}$$ example for ω: $$\omega_{ij} = 1…(1) $$ $$\omega_{ij} = \cot \alpha + \cot \beta…(2)$$
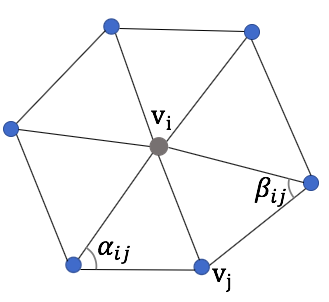
(1) is uniform weight and (2) is cotangent weight. the angle α and β are defined as follows.
The element of n×n Laplacian Matrix L is define as follows:
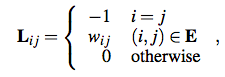
x, y, z element of Laplacian: $$\Delta_d =[\delta_{1d}, \delta_{2d},…, \delta_{2d}]^T = LV_d$$ $$d \in \{x, y, z\}$$
the discrete mean curvature normal: $$\overline{\kappa_i}n_i = \delta_{i, c\overline{\kappa_i}}$$ the discrete mean curvature: $$\overline{\kappa_i}$$ the unit length surface normal $$n_i$$
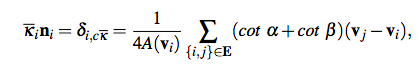
Optimization algorithm
Displaced vertices: $$V’ =[{v’}_1^T, {v’}_2^T,…, {v’}_n^T]^T$$ $$v’_i =[v’_{ix}, v’_{iy},v’_{iz}]$$
x, y, z element of V’: $$V’_d =[v’_{1d}, v’_{2d},…, v’_{nd}]^T$$ $$d \in \{x, y, z\}$$
energy to minimize:
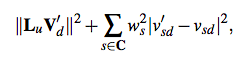
To solve the above problem, an equations of the form AV’_d = b is introduced.
1, Least squares meshes.
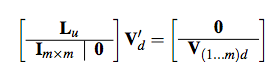
2, Detail preserving triangle shape optimization.
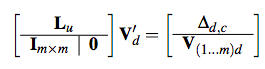
The displaced vertices are calculated by the following formula. $$V’_d =(A^TA)^{−1}A^Tb$$
Global triangle shape optimization
In this work, new general 2n×n system AV’_d = b is defined as follows.
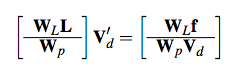
W_p is positional weight that constraints vertex position. Larger weights in
W_p preserve the original geometry.
W_L: Laplacian weight that enforce regular triangle shapes and surface smoothness.
L is Laplacian matrix(uniform, cotangent or laplacian with discrete mean curvature ). And f is the corresponding right-hand side with the diagonal matrix W_L.
Application
Check the original paper to see examples of Shape optimization and Smoothing.