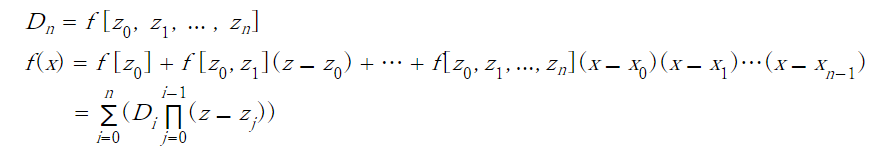What is Hermite interpolation?

GOAL

To understand Hermite interpolation.

Abstract

Hermite interpolation is one of the interpolation method that needs n points and slopes of each point.

$$nth\quad point: (x_n, f_n)$$ $$nth\quad sloop: (x_n, {f_n}^{(1)})$$

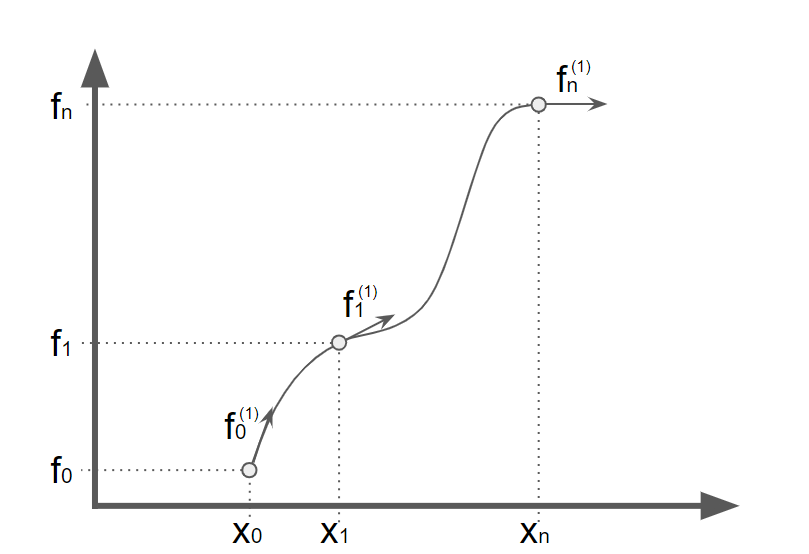
Hermite interpolation polynomial

$$f(x) = \sum_{i=0}^{n}h_{i0}(x)f_i + \sum_{i=0}^{n}h_{i1}(x){f_i}^{(1)}$$

$$h_{i0}(x) = p_i(x)[\frac{1}{p_i(x_i)} – (x – x_i) \frac {{{p_i}^{(1)}}(x_i)}{{[p_i(x_i)]}^2}$$

$$h_{i1}(x) = (x – x_i) \frac {{p_i}(x)}{{p_i}(x_i)}$$

$$p_i(x) = {(x-x_0)}^2{(x-x_1)}^2… {(x-x_{i-1})}^2{(x-x_{i+1})}^2…{(x-x_n)}^2$$

Proof

1

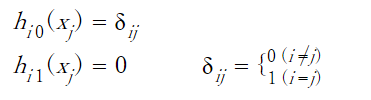
Because

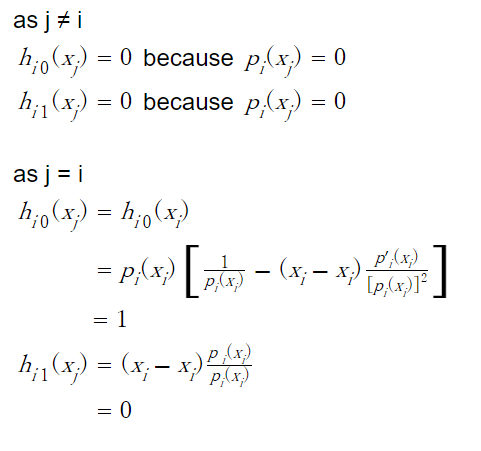
2

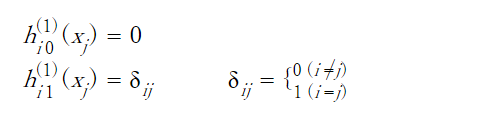
Because

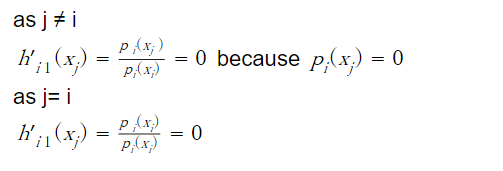
3

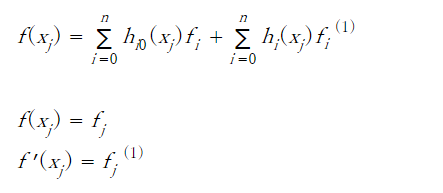
Derivation method

Derivation of interpolated function from 2 points and 2 slopes on that points. Given values are point (x_0, f(x_0)), slope f'(x_0), point (x_1, f(x_1)) and slope f'(x_1).

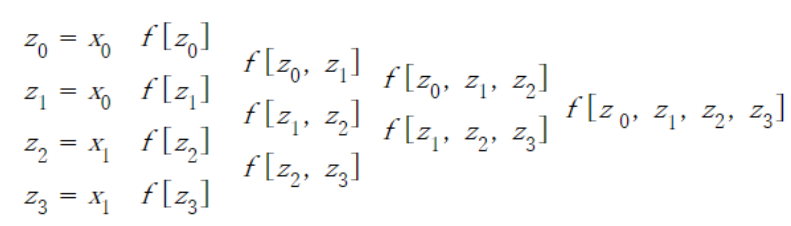
f[x], f[x, y], f[x, y, … ,z] is divided difference. Please refer to “Divided Difference” for detail.

$$f[x,x]=f'(x)$$ $$f[x_0,x_1,…,x_n]=\frac{f[x_1,x_2,…,f_n]- f[x_0,x_1,…,x_{n-1}] }{x_n-x_0}$$

f(x) is computed in the following way.