Paired One-way ANOVA And Multiple Comparisons In Python


2020-01-09 DataAnalytics Python

GOAL

To write program of paired one-way ANOVA(analysis of variance) and multiple comparisons using python. Please refer another article “Unpaired One-way ANOVA And Multiple Comparisons In Python” for unpaired one-way ANOVA.

What is ANOVA

ANOVA(analysis of variance) is a method of statistical hypothesis testing that determines the effects of factors and interactions, which analyzes the differences between group means within a sample.
Details will be longer. Please see the following site.

One-way ANOVA is ANOVA test that compares the means of three or more samples. Null hypothesis is that samples in groups were taken from populations with the same mean.

Implementation

The following is implementation example of paired one-way ANOVA.

Import Libraries

Import libraries below for ANOVA test.

import statsmodels.api as sm
from statsmodels.formula.api import ols
import pandas as pd
import numpy as np
import statsmodels.stats.anova as anova

Data Preparing

id_1id_2id_3id_4id_5id_6id_7
condition A85908869789887
condition B55826764785449
condition C46955980527370

test_data.csv

85, 90, 88, 69, 78, 98, 87
55, 82, 67, 64, 78, 54, 49
46, 95, 59, 80, 52, 73, 70

Read and Set Data

csv_line = []
with open('test_data.csv', ) as f:
    for i in f:
        items = i.split(',')
        for j in range(len(items)):
            if '\n' in items[j]:
                items[j] =float(items[j][:-1])
            else:
                items[j] =float(items[j])
        print(items)
        csv_line.append(items)
groupA = csv_line [0]
groupB = csv_line [1]
groupC = csv_line [2]
tdata = pd.DataFrame({'A':groupA, 'B':groupB, 'C':groupC})
tdata.index = range(1,10)
tdata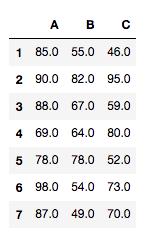

If you want to display data summary, use DataFrame.describe().

tdata.describe()

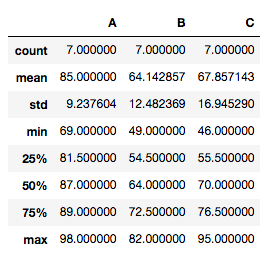
ANOVA

subjects=['id1','id2','id3','id4','id5','id6','id7']
points = np.array(groupA +groupB + groupC)
conditions = np.repeat(['A','B','C'],len(group0))
subjects = np.array(subjects+subjects+subjects)
df = pd.DataFrame({'Point':points,'Conditions':conditions,'Subjects':subjects})
aov=anova.AnovaRM(df, 'Point','Subjects',['Conditions'])
result=aov.fit()

print(result)

>>                 Anova
========================================
           F Value Num DF  Den DF Pr > F
----------------------------------------
Conditions  5.4182 2.0000 12.0000 0.0211
========================================

The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.
When statistically significant, that is, p-value is less than 0.05 (typically ≤ 0.05), perform a multiple comparison. This p value is different between paired ANOVA and unpaired ANOVA.

Tukey’s multiple comparisons

Use pairwise_tukeyhsd(endog, groups, alpha=0.05) for tuky’s HSD(honestly significant difference) test. Argument endog is response variable, array of data (A[0] A[1]… A[6] B[1] … B[6] C[1] … C[6]). Argument groups is list of names(A, A…A, B…B, C…C) that corresponds to response variable. Alpha is significance level.

def tukey_hsd(group_names , *args ):
    endog = np.hstack(args)
    groups_list = []
    for i in range(len(args)):
        for j in range(len(args[i])):
            groups_list.append(group_names[i])
    groups = np.array(groups_list)
    res = pairwise_tukeyhsd(endog, groups)
    print (res.pvalues) #print only p-value
    print(res) #print result
print(tukey_hsd(['A', 'B', 'C'], tdata['A'], tdata['B'],tdata['C']))
>> [0.02259466 0.06511251 0.85313142]
 Multiple Comparison of Means - Tukey HSD, FWER=0.05 
=====================================================
group1 group2 meandiff p-adj   lower    upper  reject
-----------------------------------------------------
     A      B -20.8571 0.0226 -38.9533 -2.7609   True
     A      C -17.1429 0.0651 -35.2391  0.9533  False
     B      C   3.7143 0.8531 -14.3819 21.8105  False
-----------------------------------------------------
None