What Is Convolution In Neural Network?
GOAL
Today’s goal is to understand a layer of process “convolution” in neural network. In other words, this article describes convolutional neural network (CNN or ConvNet) that is a neural network contains convolutional layers in its architecture.
What Convolution Is
Convolution is the binary operation to takes 2 functions and produces a function \(f * g\), which is defined as the integral of the product of the two functions after one is reversed and shifted.
$$(f*g)(t) = \int f(\tau)g(t – \tau)d\tau $$
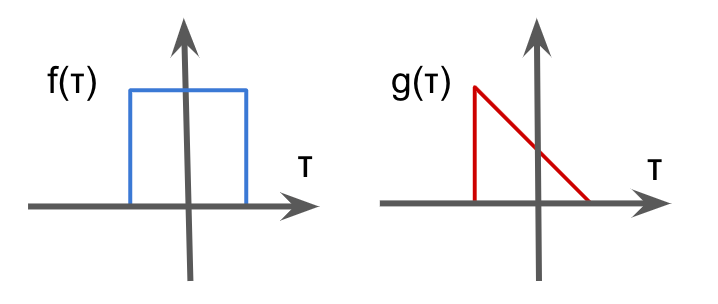
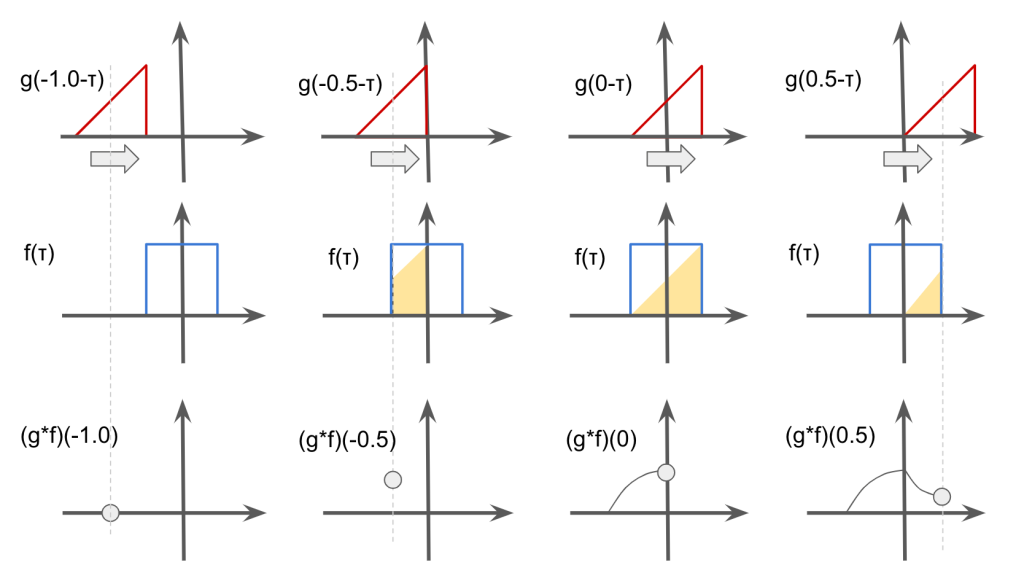
In the context of image processing, convolution is the process of generating output image by weighting input image with the filter. For example, convolution is used in smoothing with gaussian filter.
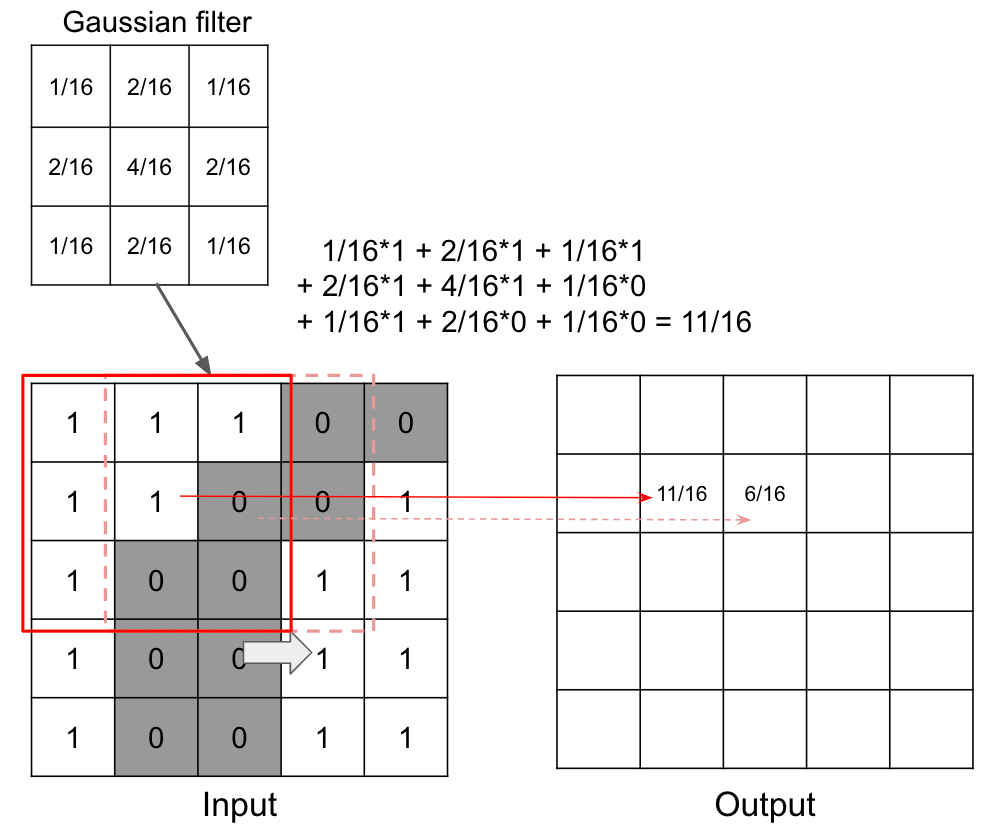
The image of weights is called “kernel” in convolution. And the output is the compression of input.
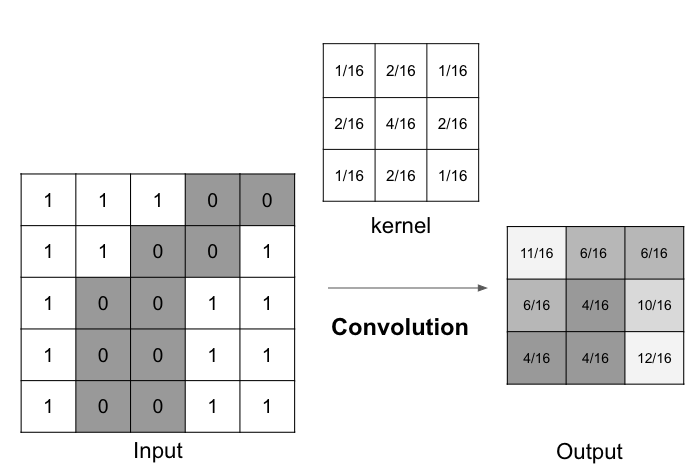
In CNN, the convolution layer is used to generate output image that represents feature of input image while compressing local region. 1 layer can have several kernels and the output is the same number of feature maps as kernels.
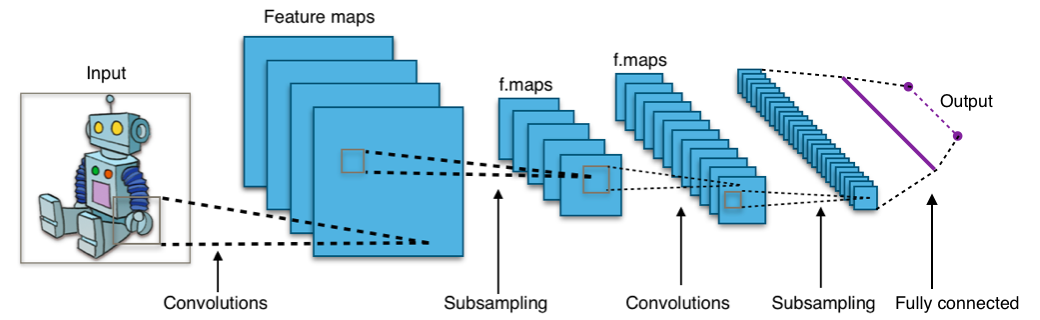
by Aphex34
Details Of Convolution Layer
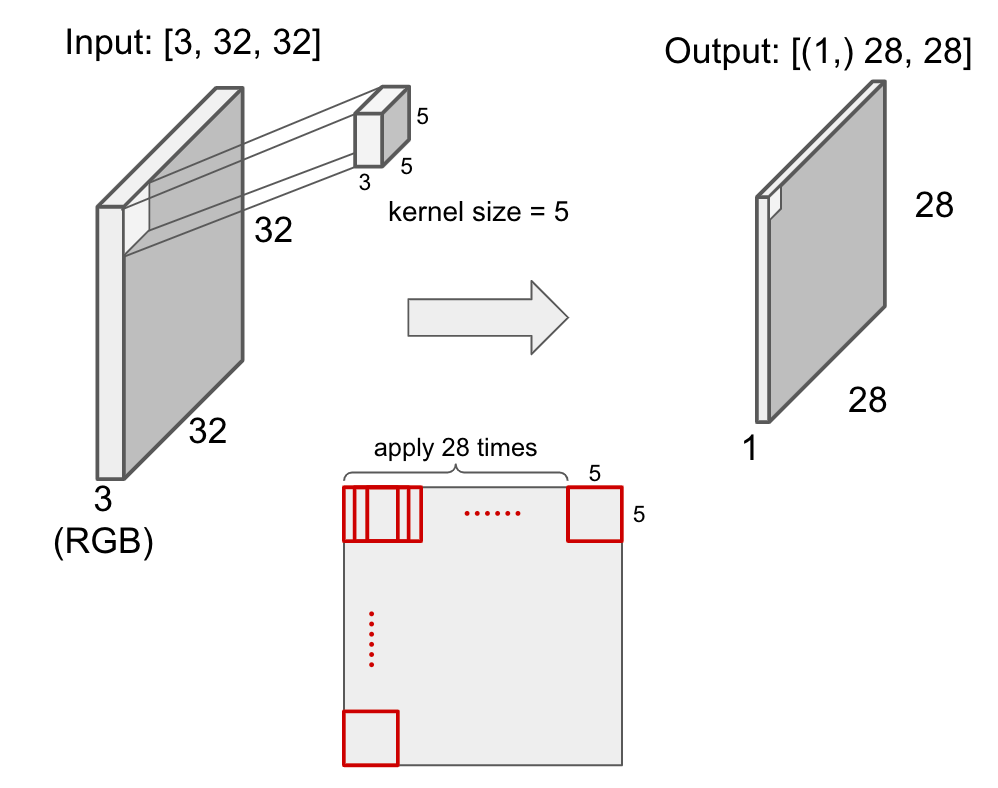
In convolution layer, the input image will be converted. For example, a 5*5 kernel is applied to RGB 32*32 image to generate 28*28 output as below.
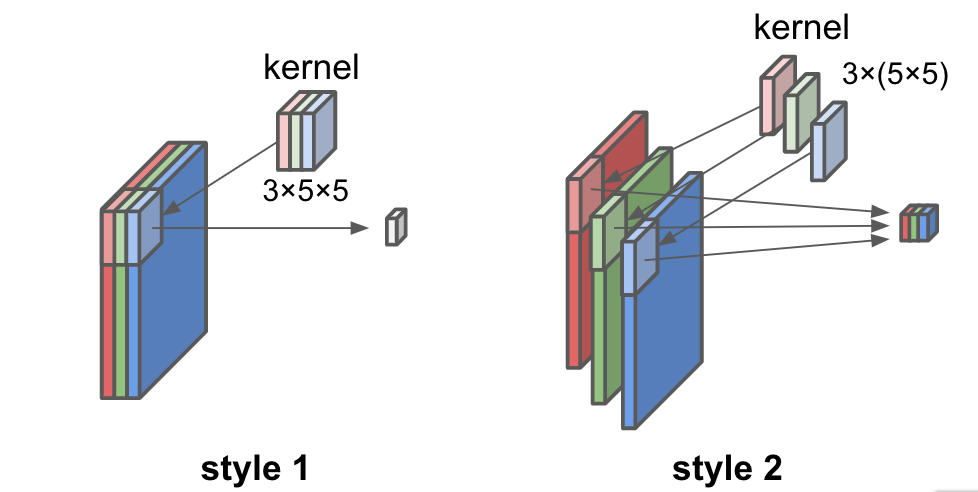
Note that there are 2 styles of convolution for RGB image. The first one is the way in which 3 maps generated from RGB channels by convolution are added together to 1 channel output image. In the second way, each channel is converted to each channel of output image. In the latter case the output image has 3 channels.
The former is commonly used in CNN.
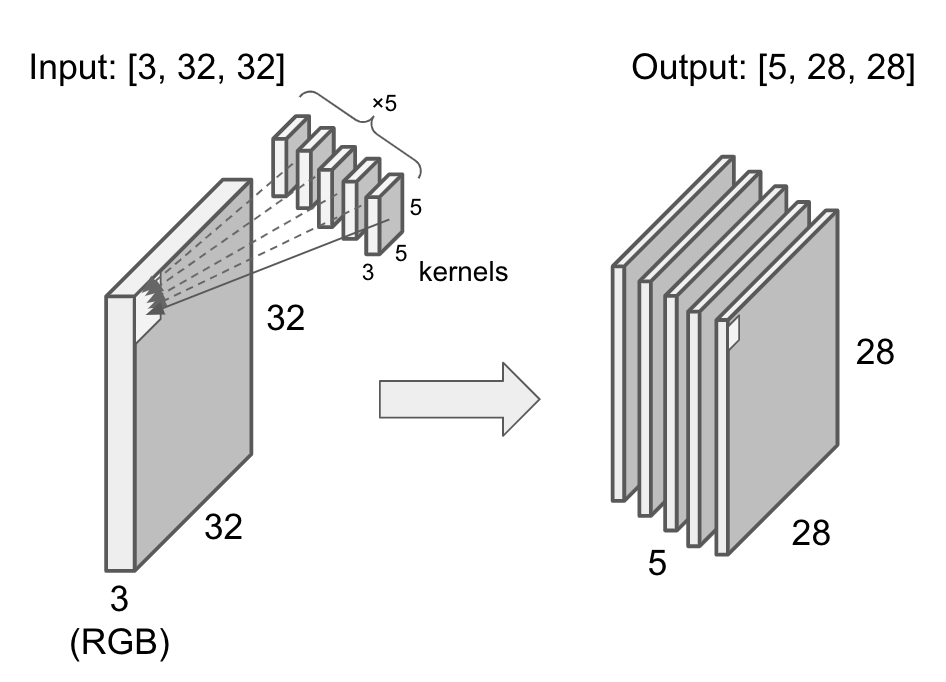
If the convolution layer has 5 different kernels, the output has 5 channels.
Parameters
Parameters that determines convolution process.
- channel
- kernel size
- stride
- padding
- dilation
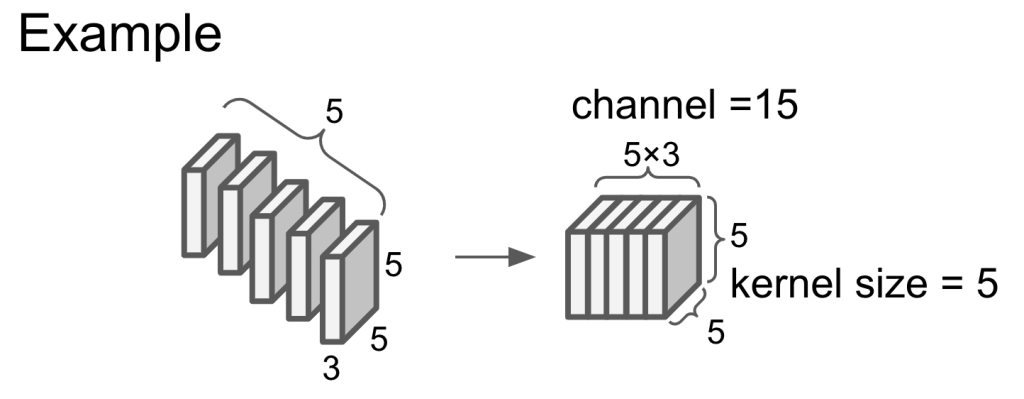
Channel and kernel size
channel = input channel * the number of kernel. The channel of output is the same as the channel of kernel.
Kernel size is the size of kernel side.
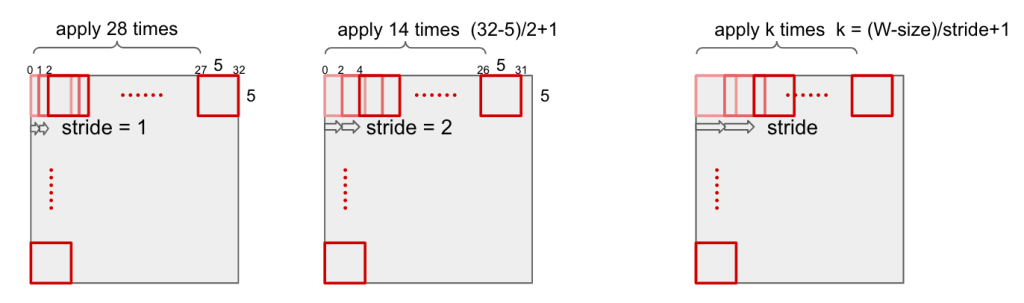
Stride
Stride is the size that filter sliding to input image.
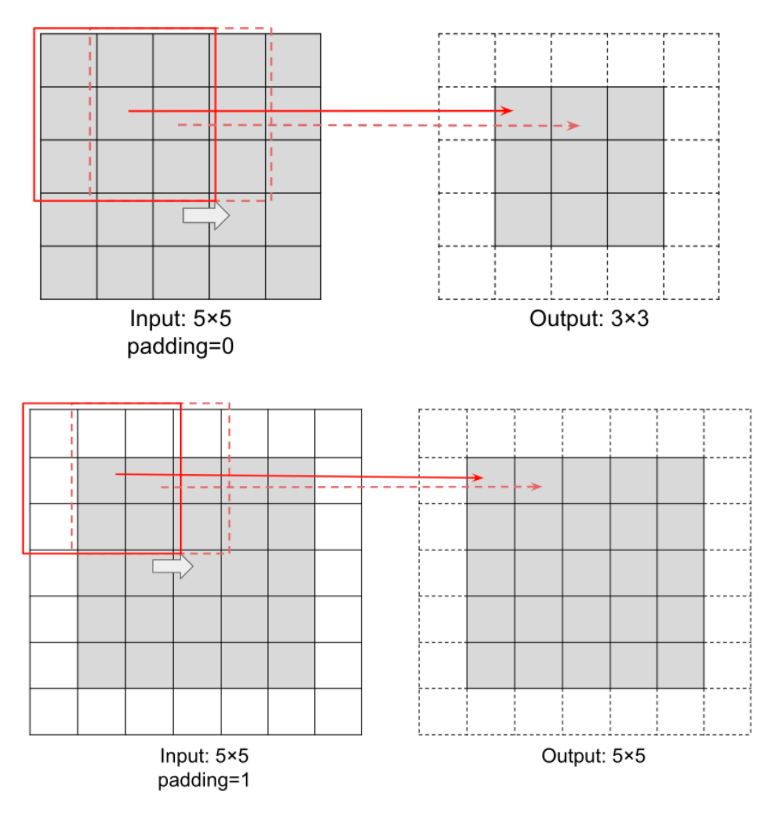
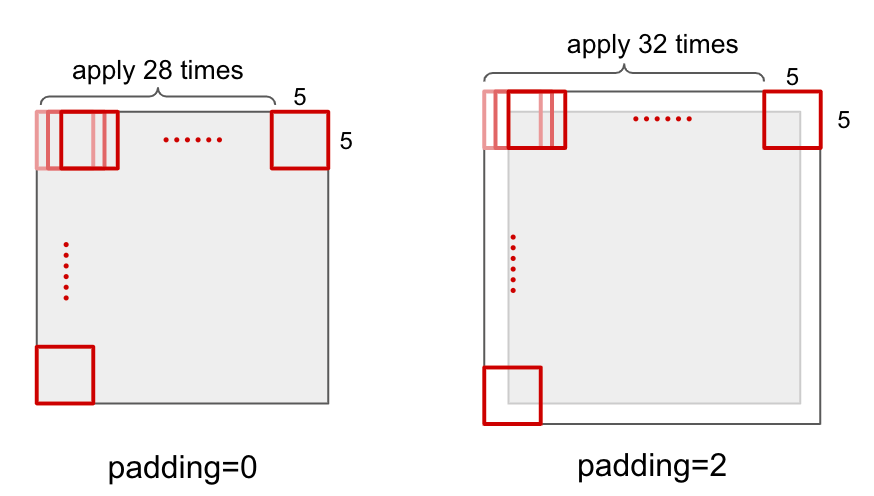
Padding
Padding is the amount of padding space applied on both sides of input. Padding changes output size to fit input image size.
Dilation
Dilation controls the spacing between the kernel points.
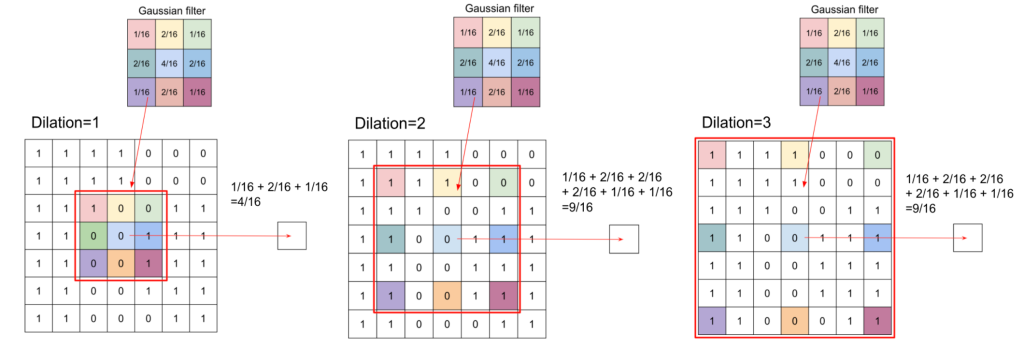
Convolution In PyTorch
PytTorch provides a method torch.nn.Conv2d() for 2D convolution. Conv2d makes a convolutional layer in network class that extends nn.Module as below.
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 3) #1channel input, 6channel output (6kernels), 3*3 kernel
self.conv2 = nn.Conv2d(6, 16, 3) #6channel input, 16channel output, 3*3 kernel
self.fc1 = nn.Linear(16 * 6 * 6, 120) #Linear transform from 16*6*6 features into 84 features
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, (2, 2))
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:]
num_features = 1
for s in size:
num_features *= s
return num_flat_features
net = Net()See the detail of net architecture by print().
print(net) ——outout—— Net( (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1)) (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1)) (fc1): Linear(in_features=576, out_features=120, bias=True) (fc2): Linear(in_features=120, out_features=84, bias=True) (fc3): Linear(in_features=84, out_features=10, bias=True) )
See the size of parameters in conv1 and conv2.
params = list(net.parameters()) print(params[0].size()) print(params[2].size()) ——outout—— torch.Size([6, 1, 3, 3]) torch.Size([16, 6, 3, 3])