Union-Find in Python

GOAL

To understand and to implement union-find in Python.

Example of problems using union-find algorithm

Dividing clusters

There is a list of friends from N people. Divide them in cluster.

n = 6
friendship = [(1, 2), (3, 4), (1, 6)]

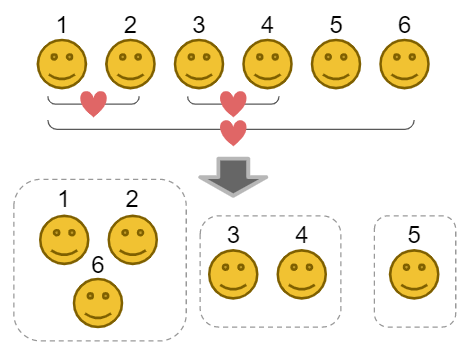
Questions:
Are person 2 and person 3 in the same cluster?
How many members in the cluster which person 3 belongs to?

Connected Path

nodes = 10
adjacency_list = [[6, 8], [2, 3], [1], [1], [5, 7], [4, 7], [0], [4, 5, 9], [0], [7]]
# => connections = [(0, 6), (0, 8), (1, 2), (1, 3), (4, 5), (4, 7), (5, 7), (7, 9)]

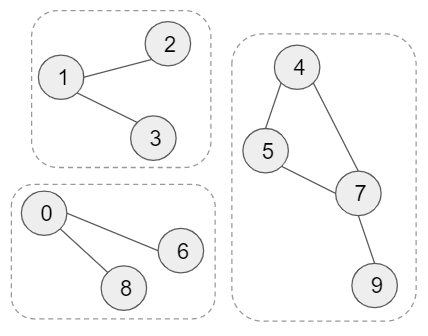
Questions:
Is there any path from 2 to 3?
How many connected graphs are there?

What is Union-Find algorithm?

Union-Find algorithm is the algorithm to handle disjoint-set data structure.

Uinion(x, y): Connect x and y. Marge the group which x belongs to and the group which y belongs to.
Find(x): Find the group which x belongs to.

Please refer to Basics of Disjoint Data Structures for the more description. This article is easy to understand and detailed.

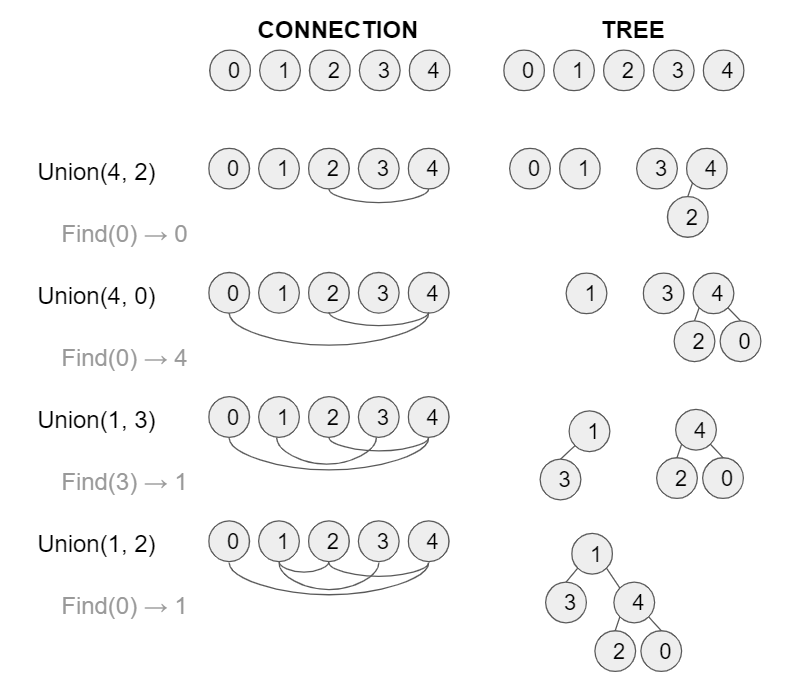
Example of implementation

I’ll introduce a method to implement union-find algorithm using lists “rank” and “parent”. The below is overview.

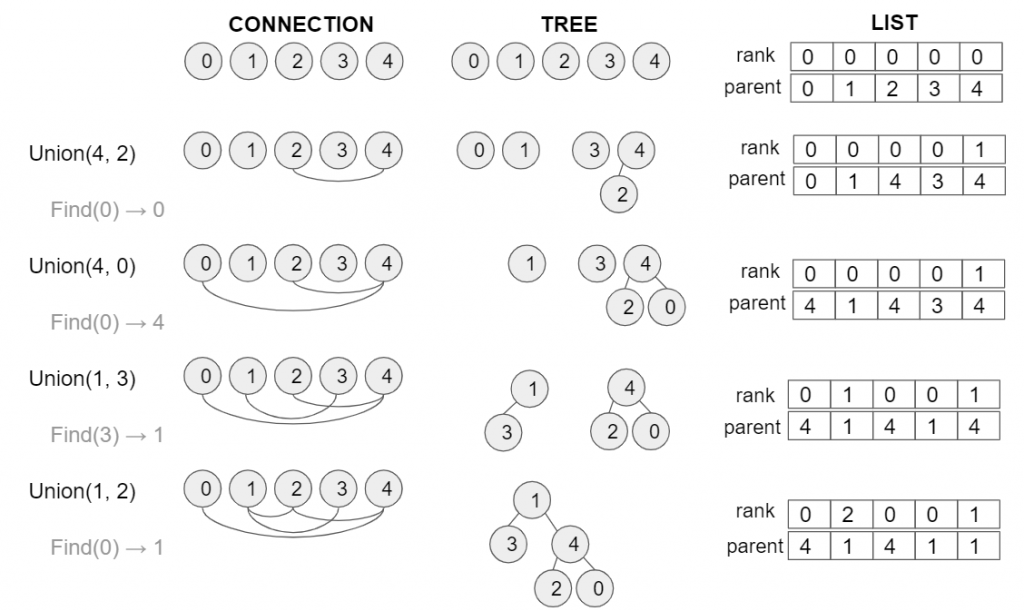
class UnionFind:
    def __init__(self, size):
        self.rank = [0 for i in range(size)]
        self.parent = [i for i in range(size)]
    
    def Find(self, x):
        parent = self.parent[x]
        while parent != x:
            x = parent
            parent = self.parent[x]
        return parent
    
    def Union(self, x, y):
        root_x = self.Find(x)
        root_y = self.Find(y)
        if root_x == root_y:
            return
        else:
            if self.rank[root_x] >= self.rank[root_y]:
                self.parent[root_y] = root_x
                self.rank[root_x] = max(self.rank[root_y] + 1, self.rank[root_x])
            else:
                self.parent[root_x] = root_y
                self.rank[root_y] = max(self.rank[root_x] + 1, self.rank[root_y])
    def Same(self, x, y):
        return self.Find(x) == self.Find(y)

unionfind = UnionFind(5)

unionfind.Union(4, 2)
# rank [0, 0, 0, 0, 1], parent [0, 1, 4, 3, 4]
print(unionfind.Find(0))
# 0
unionfind.Union(4, 0)
# rank [0, 0, 0, 0, 1]k, parent [4, 1, 4, 3, 4]
print(unionfind.Find(0))
# 4
unionfind.Union(1, 3)
# rank [0, 1, 0, 0, 1], parent [4, 1, 4, 1, 4]
print(unionfind.Find(3))
# 1
unionfind.Union(1, 2)
# rank [0, 2, 0, 0, 1], parent [4, 1, 4, 1, 1]
print(unionfind.Find(0))
# 1

Variation

Find root and get the size of the tree

Change the list “parent” so that it returns the parent or the size of tree. And if the item is the root of tree, it returns the size of the tree. To identify the value of the element is the root or the size, the size is stored as negative number. For example, when 2 is the root of the tree with the size 5, parent[2] is -5.

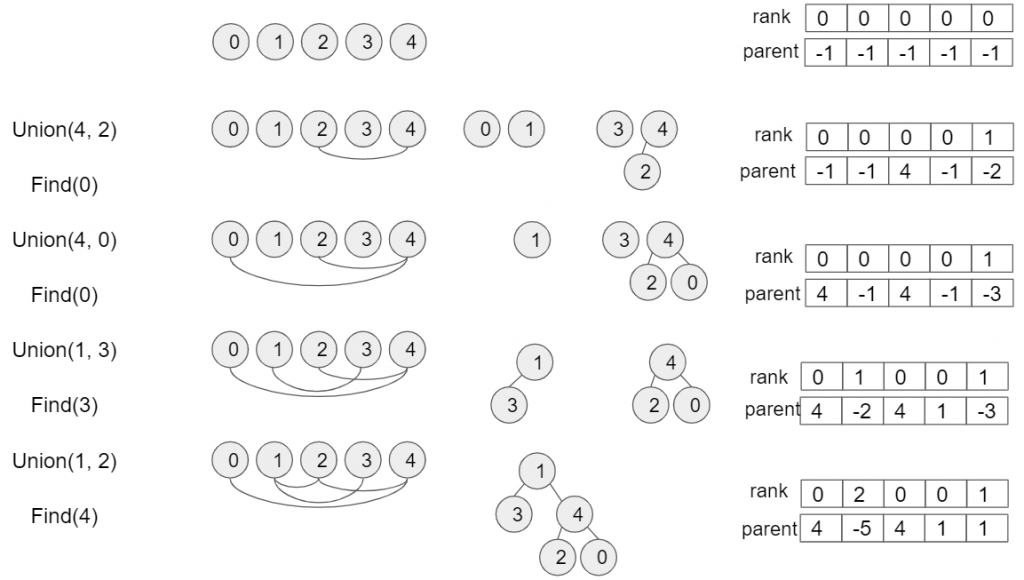
class UnionFind:
    def __init__(self, size):
        self.rank = [0 for i in range(size)]
        self.parent = [-1 for i in range(size)]
    
    def Find(self, x):
        parent = self.parent[x]
        while parent >= 0:  #termination condition has changed
            x = parent
            parent = self.parent[x]
        return x
    
    def Union(self, x, y):
        root_x = self.Find(x)
        root_y = self.Find(y)
        if root_x == root_y:
            return
        else:
            if self.rank[root_x] >= self.rank[root_y]:
                self.parent[root_x] += self.parent[root_y]  #parent[root_id] is always negative
                self.parent[root_y] = root_x
                self.rank[root_x] = max(self.rank[root_y] + 1, self.rank[root_x])
            else:
                self.parent[root_y] += self.parent[root_x]
                self.parent[root_x] = root_y
                self.rank[root_y] = max(self.rank[root_x] + 1, self.rank[root_y])
    def Same(self, x, y):
        return self.Find(x) == self.Find(y)
    def FindRootAndSize(self):
        return [(idx, -val) for idx, val in enumerate(self.parent) if val<0 ]

unionfind = UnionFind(5)

unionfind.Union(4, 2)
unionfind.Union(4, 0)
unionfind.Union(1, 3)
print(unionfind.FindRootAndSize())
# [(1, 2), (4, 3)]
unionfind.Union(1, 2)
print(unionfind.FindRootAndSize())
# [(1, 5)]

Find all items in the tree

Add list “children” to store children items and itself.

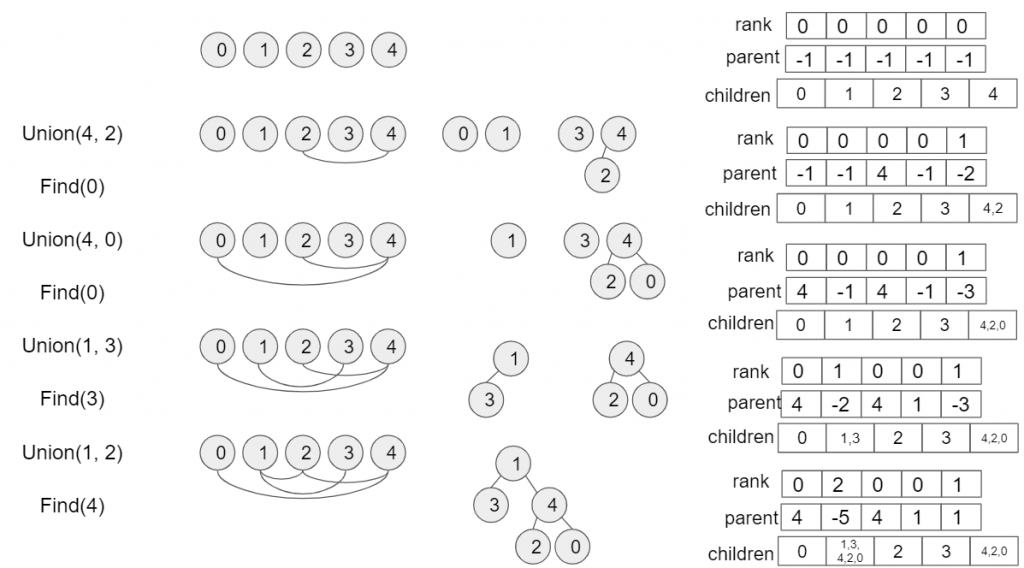
class UnionFind:
    def __init__(self, size):
        self.rank = [0 for i in range(size)]
        self.parent = [-1 for i in range(size)]
        self.children = [[i] for i in range(size)]
    
    def Find(self, x):
        parent = self.parent[x]
        while parent >= 0:
            x = parent
            parent = self.parent[x]
        return x
    
    def Union(self, x, y):
        root_x = self.Find(x)
        root_y = self.Find(y)
        if root_x == root_y:
            return
        else:
            if self.rank[root_x] >= self.rank[root_y]:
                self.parent[root_x] += self.parent[root_y]
                self.parent[root_y] = root_x
                self.rank[root_x] = max(self.rank[root_y] + 1, self.rank[root_x])
                self.children[root_x] += self.children[root_y]
            else:
                self.parent[root_y] += self.parent[root_x]
                self.parent[root_x] = root_y
                self.rank[root_y] = max(self.rank[root_x] + 1, self.rank[root_y])
                self.children[root_y] += self.children[root_x]
    def Same(self, x, y):
        return self.Find(x) == self.Find(y)
    def FindRootAndSizeAndChildren(self):
        return [(idx, -val, self.children[idx]) for idx, val in enumerate(self.parent) if val<0 ]

unionfind = UnionFind(5)

unionfind.Union(4, 2)
unionfind.Union(4, 0)
unionfind.Union(1, 3)
print(unionfind.FindRootAndSizeAndChildren())
# [(1, 2, [1, 3]), (4, 3, [4, 2, 0])]
unionfind.Union(1, 2)
print(unionfind.FindRootAndSizeAndChildren())]
# [(1, 5, [1, 3, 4, 2, 0])]