Internal Representation of Numbers in Computer.

I found the following phenomena but why?

#source code
a = 1.2
b = 2.4
c = 3.6
print(a + b == c)

False

GOAL

To understand the mechanism of the internal representation of integer and float point in computer.

Binary Number

Numbers are represented as binary number in computer.

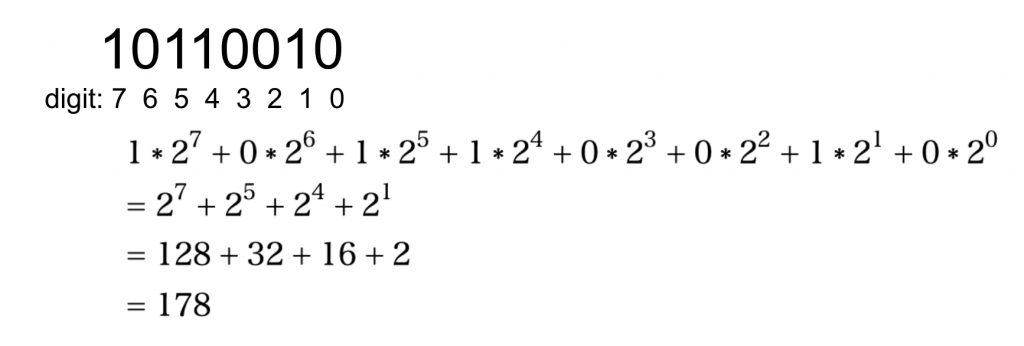
Unsigned int

Signed int: Two’s Complement notation

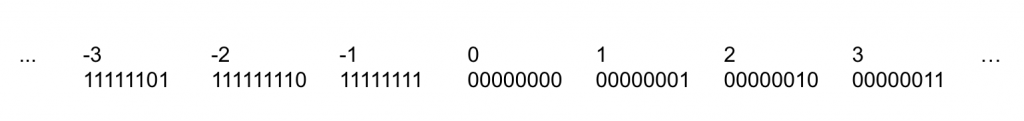
What is complement?

Complement has two definition.
First, complement on n of a given number can be defined as the smallest number the sum of which and the given number increase its digit. Second, it is also defined as the biggest number the sum of which and the given number doesn’t increase its digit. In decimal number, the 10’s complement of 3 is 7 and the 9’s complement of 3 is 6. How about in binary number?

One’s complement

One’s complement of the input is the number generated by reversing each digit of the input from 0 to 1 and from 1 to 0.

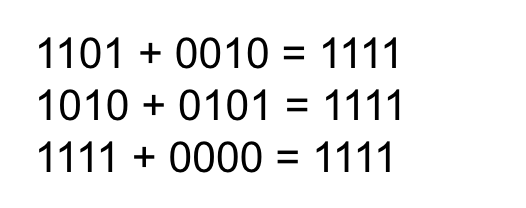
Two’s complement

Two’s complement of the input is the number generated by reversing each digit of the input, that is one’s complement, plus 1. Or it can be calculated easily by subtracting 1 from the input and reverse each digit from 1 to 0 and from 0 to 1.

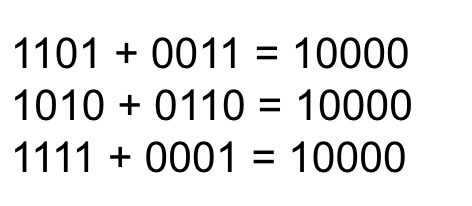
The range that can be expressed in two’s complement notation

The range is asymmetric.

Floating point

The following is the way to represent floating point number in computer.

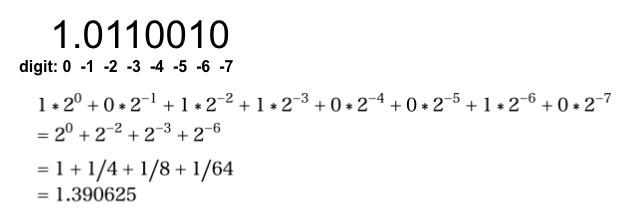
The digit is limited and this means that the floating point can’t represent all the decimals in continuous range. Then the decimals are approximated to closest numbers.

Why float(1.2)＋float(2.4) is not equal to float(3.6)?

In computers float number can’t have exactly 1.1 but just an approximation that can be expressed in binary. You can see errors by setting the number of decimal places bigger.

#source code
a = 1.2
b = 2.4
c = 3.6
print('{:.20f}'.format(a))
print('{:.20f}'.format(b))
print('{:.20f}'.format(c))
print('{:.20f}'.format(a+b))

1.19999999999999995559
2.39999999999999991118
3.60000000000000008882
3.59999999999999964473

*You can avoid this phenomena by using Decimal number in python.

from decimal import *
a = Decimal('1.2')
b = Decimal('2.4')
c = Decimal('3.6')
print(a+b == c)

print('{:.20f}'.format(a))
print('{:.20f}'.format(b))
print('{:.20f}'.format(c))
print('{:.20f}'.format(a+b))

True
1.20000000000000000000
2.40000000000000000000
3.60000000000000000000
3.60000000000000000000