Discrete Differential-Geometry Operators for Triangulated 2-Manifolds
Today I’ve read the paper “Discrete Differential-Geometry Operators
for Triangulated 2-Manifolds” by Mark Meyer, Mathieu Desbrun, Peter Schröder, Alan H. Barr.
Novelty of the study
Deriving first and second order operators at the vertices of a mesh using the 1-ring(star neighborhood). In other words, providing the way to extend the definition of curvature from continuous surfaces to discrete meshes.
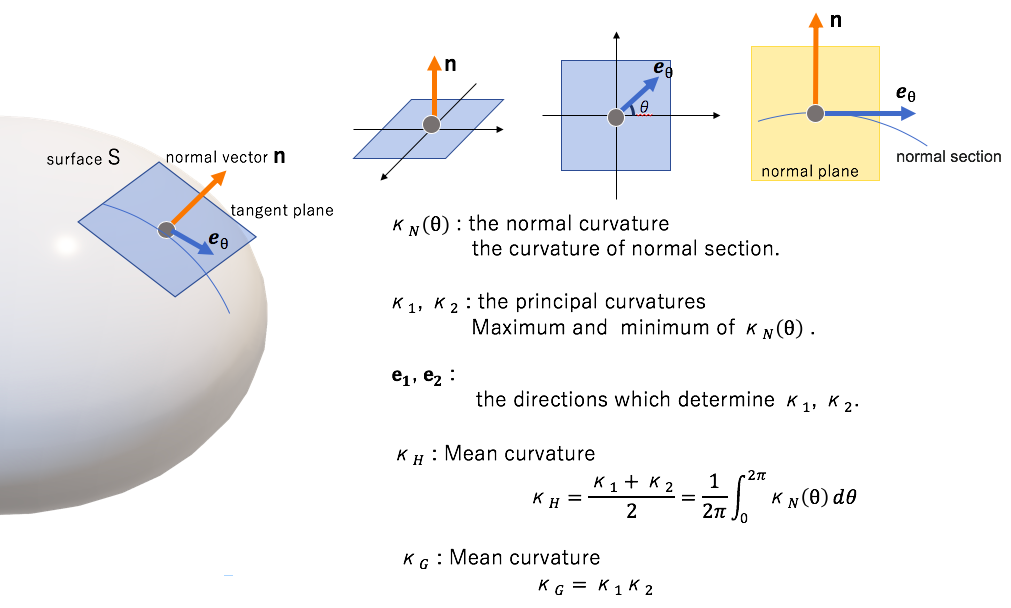
Definitions of the curvature in continuous surface
The normal curvature and related notions are defined as follows.
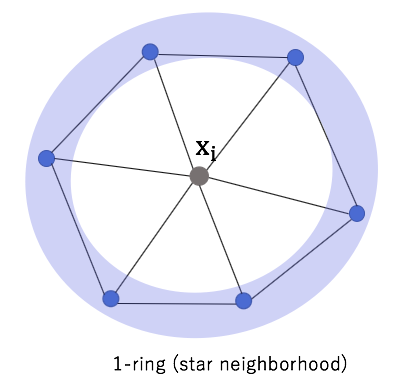
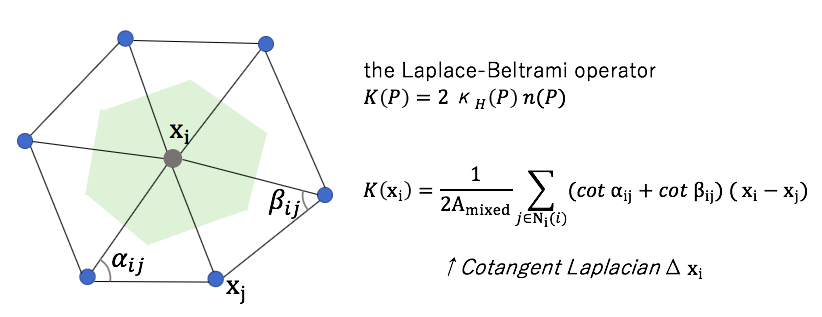
Approximation
The average calculation is restricted to be within the immediately neighboring triangles referred as the 1-ring.
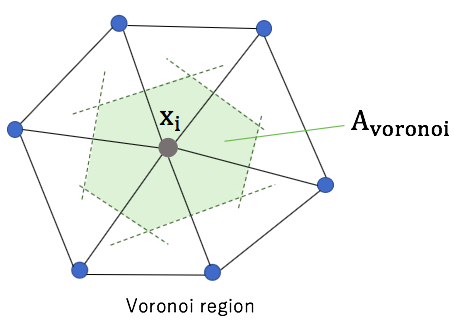
The voronoi region is used as small area around point xi.
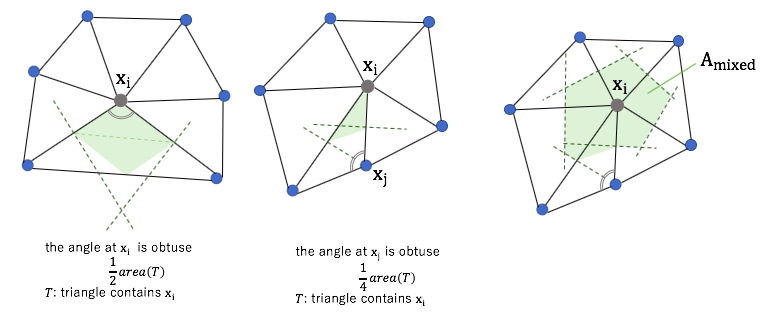
However, the formula for the Voronoi finite-volume area does not hold in the presence of obtuse angles. So mixed area is used in the actual calculation.
The Laplace-Beltrami operator K is computed.
The Laplace-Beltrami operator (the mean curvature normal operator) is a generalization of the Laplacian from flat spaces to manifolds.
Derivation
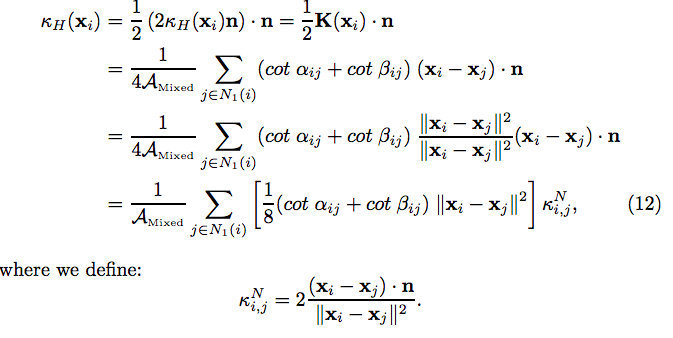
for Triangulated 2-Manifolds”
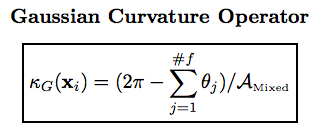
for Triangulated 2-Manifolds”

for Triangulated 2-Manifolds”