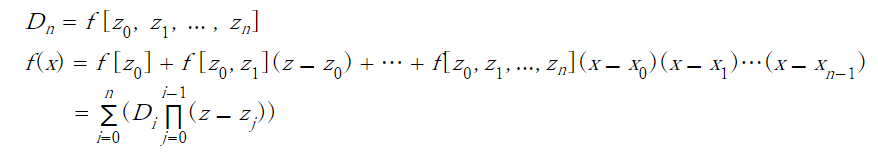What is Hermite interpolation?

GOAL

To understand Hermite interpolation.

Abstract

Hermite interpolation is one of the interpolation method that needs n points and slopes of each point.

$$ nth\quad point: (x_n, f_n)$$ $$nth\quad sloop: (x_n, {f_n}^{(1)})$$

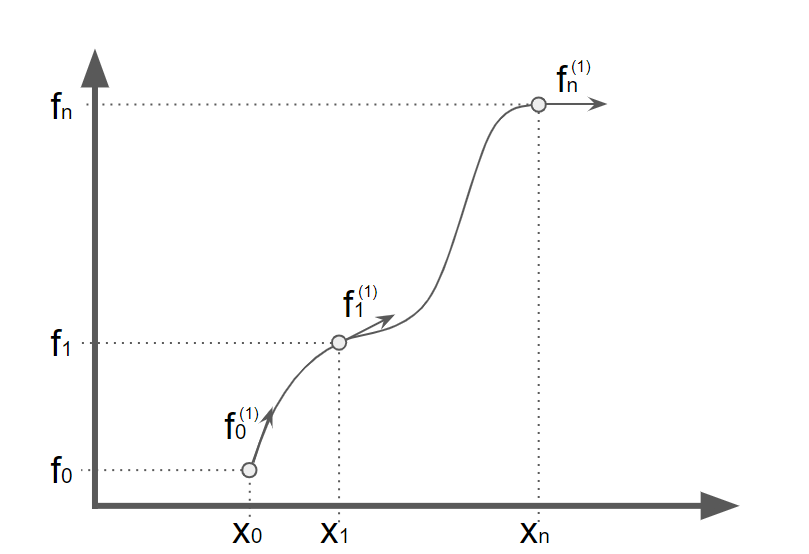
Hermite interpolation polynomial

$$f(x) = \sum_{i=0}^{n}h_{i0}(x)f_i + \sum_{i=0}^{n}h_{i1}(x){f_i}^{(1)}$$

$$h_{i0}(x) = p_i(x)[\frac{1}{p_i(x_i)} – (x – x_i) \frac {{{p_i}^{(1)}}(x_i)}{{[p_i(x_i)]}^2}$$

$$h_{i1}(x) = (x – x_i) \frac {{p_i}(x)}{{p_i}(x_i)}$$

$$p_i(x) = {(x-x_0)}^2{(x-x_1)}^2… {(x-x_{i-1})}^2{(x-x_{i+1})}^2…{(x-x_n)}^2$$

Proof

1

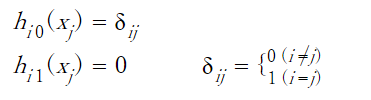
Because

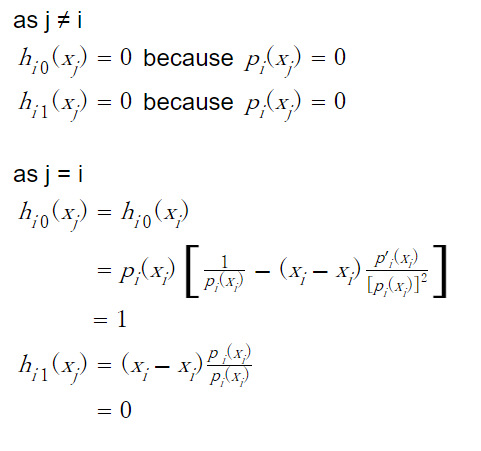
2

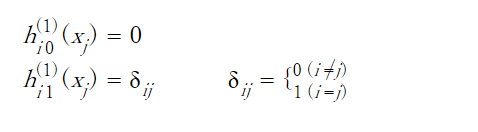
Because

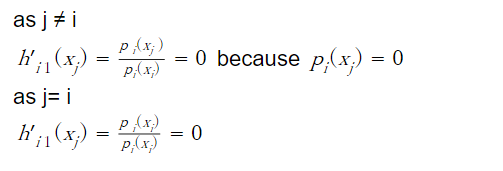
3

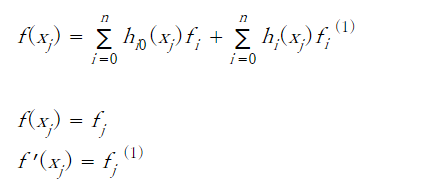
Derivation method

Derivation of interpolated function from 2 points and 2 slopes on that points. Given values are point (x_0, f(x_0)), slope f'(x_0), point (x_1, f(x_1)) and slope f'(x_1).

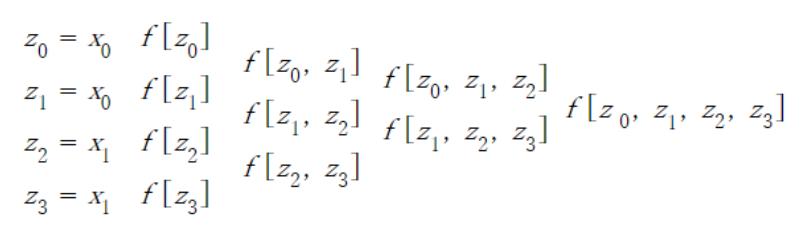
f[x], f[x, y], f[x, y, … ,z] is divided difference. Please refer to “Divided Difference” for detail.

$$f[x,x]=f'(x)$$ $$f[x_0,x_1,…,x_n]=\frac{f[x_1,x_2,…,f_n]- f[x_0,x_1,…,x_{n-1}] }{x_n-x_0}$$

f(x) is computed in the following way.

Divided Difference

GOAL

To understand what “divided difference” is.

POINTS

The divided difference is the difference between the values ​of functions divided by the difference of the arguments. The higher-order divided difference is the divided difference of the divided difference.

DEFINITION

0th divided difference

$$f[x_0] = f(x_0)$$

1st divided difference

$$f[x_0, x_1] = \frac{ f(x_0)-f(x_1)}{x_0-x_1}$$

2nd divided difference

$$f[x_0, x_1, x_2] = \frac{ f[x_0, x_1] – f[x_1, x_2] }{x_0-x_2}$$

Generalized nth divided difference

$$f[x_0, … x_n] = \frac{ f[x_0, … x_{n-1}] – f[x_1, … x_n] }{x_0 – x_n}$$

PROPERTIES

Linearity

$$(f+g)[x_0, … x_n] = f[x_0, … x_n] + g[x_0, … x_n]$$

Symmetry

σ is one of the permutations.

$$σ = \begin{pmatrix} 0 & 1 & … & n \\ σ(0) & σ(1) & … &σ(n)\end{pmatrix}$$

$$f[x_0, x_1, …, x_n] = f[σ(0), σ(1), … ,σ(n)]$$

Relationship with the derivative

$$f'(x) = \frac{df}{dx} = \lim_{h \to 0}f[x + h, x]$$